Programming Overview¶
A programming language involves defining a minimu set of instructions that a computer can understand and execute.
- Input/Output: Implement input and output operations for user interaction. For instance:
user_input = input("Enter a value: ")
print("Output: ", user_input)
- Assignment: Define a way to assign values to variables. For example:
variable_name = value
- Arithmetic Operations: Implement basic arithmetic operations such as addition, subtraction, multiplication, and division. For instance:
result = a + b
- $Conditional Statements$: Include conditional statements for decision-making. For example:
if condition:
code to execute if the condition is true
else:
code to execute if the condition is false
- $Loops$: Create loops for repetitive tasks. For instance:
while condition:
code to repeat while the condition is true
- $Functions$: Define functions to encapsulate reusable blocks of code. For example:
def function_name(parameters):
function code
return result
Functions¶
In programming, a function is a reusable, self-contained block of code that performs a specific task or set of tasks. Functions are fundamental to modular programming, allowing developers to break down a program into smaller, manageable pieces.
A function is a block of code that can run when it is called aka parenthesis () after the function name.
A function can have input arguments, information usefull to its run.
A functions can also have output parameters, which are the results of the function that the user expects to receive.
We saw many built-in Python functions already, such as type, len, and so on. Also we saw the functions from some packages, for example, math.sin, Torino.team.
Few examples:
- the function $len$ has one input argument (a collection), and one output parameter (the number of item in the collection)
- the function $team$ of module Torino has one input argument (player name), and no output
- the function $now$ of module datetime from library datetime has no input argument, and one output parameter (time)
import Torino
from datetime import datetime
a = [2,4,'t',{}]
out1 = len(a)
print('out1= ', out1)
out2 = Torino.team('Bruno')
print('out2= ', out2)
out3= datetime.now()
print('out3= ', out3)
out1= 4 player = Bruno out2= None out3= 2023-12-14 16:57:36.205080
Define your own function¶
We can define our own functions. A function can be specified in several ways. Here we will introduce the most common way to define a function which can be specified using the keyword def, as showing in the following:
def function_name(argument_1, argument_2, ...):
'''
Descriptive String
'''
# comments about the statements
function_statements
return output_parameters (optional)
We could see that defining a Python function need the following two components:
Function header: A function header starts with a keyword def, followed by a pair of parentheses with the input arguments inside, and ends with a colon (:)
Function Body: An indented (usually four white spaces) block to indicate the main body of the function. It consists 3 parts:
- Descriptive string: A string that describes the function that could be accessed by the help() function or the question mark. You can write any strings inside, it could be multiple lines.
- Function statements: These are the step by step instructions the function will execute when we call the function. You may also notice that there is a line starts with '#', this is a comment line, which means that the function will not execute it.
- Return statements: A function could return some parameters after the function is called, but this is optional, we could skip it. Any data type could be returned, even a function, we will explain more later.
def count_different_vowels(in_string):
""" Returns the number of different vowels contained in `in_string`"""
vowels = set("AEIOU")
out = set(in_string.upper()) & vowels
return len(out)
count_different_vowels(" Returns the number of different vowels contained in `in_string`")
5
LAMBDA¶
Sometimes, we don’t want to use the normal way to define a function, especially if our function is just one line. In this case, we can use anonymous function in Python, which is a function that is defined without a name. This type of functions also called labmda function, since they are defined using the labmda keyword. A typical lambda function is defined:
lambda arguments: expression
It can have any number of arguments, but with only one expression.
# check if a number is even
is_even = lambda x: x % 2 == 0
is_even(9)
False
Branching Statements¶
When writing functions, it is very common to want certain parts of the function body to be executed only under certain conditions. For example, depending from types parameters a different set of instruction should be executed.
def assess_age(age):
if age < 0:
return "Invalid age"
elif 0 <= age < 18:
return "Minor"
elif 18 <= age < 65:
return "Adult"
else:
return "Senior"
assess_age(24)
'Adult'
Iteration¶
Many tasks in life are boring or tedious because they require doing the same basic actions over and over again—iterating—in slightly different contexts. For example, consider looking up the definition of 20 words in the dictionary, populating a large EXCEL table with data, alphabetizing many stacks of paper, or dusting off every object and shelf in your room. Since repetitive tasks appear so frequently, it is only natural that programming languages like Python would have direct methods of performing iteration. In Python two type of loop are available:
- $for$ loop
- $while$ loop
FOR-Loop¶
A for-loop is a set of instructions that is repeated, or iterated, for every value in a collection (list, dict,tuple, set etc). The general syntax of a for-loop block is as follows.
for looping variable in sequence:
code block
# loop that sum the double of all the number in a a list if number are positives
total = 0 # outside the loop
for num in (-22.0, 3.5, 8.1, -10, 0.5):
if num > 0: # Inside the loop
total = total + 2*num # Inside the branching
print(total) # inside the loop
print('\n\n',total) # outside the loop
0 7.0 23.2 23.2 24.2 24.2
Attention Python requires indentation to define statement blocks
WHAT IS HAPPENING?¶
- The variable total is assigned the value 0
- The variable num is assigned the value -22.0.
- num is less than 0, it continue the cycle
- The variable num is assigned the value 3.5.
- num >0
- The variable total is assigned to value of 0 + 2*3.5 = 7.0
- The variable num is assigned the value 8.1.
- num >0
- The variable total is assigned to value of 7.0 + 2*8.1 = 23.2
- The variable num is assigned the value -10.0.
- num is less than 0, it continue the cycle
...
To loop on dictionary, if the loop in not explicit it will loop on keys. It is better to explicit using method $keys()$ or $values()$ It is possible loop over keys and values using $items()$ method.
grocery_prices = {
'apple': 1.25,
'banana': 0.75,
'orange': 1.00,
'bread': 2.50,
'milk': 1.80,
'eggs': 2.20,
'chicken': 5.50,
'potatoes': 1.50,
'tomatoes': 2.00,
'onions': 0.80
}
# print the dictionary with all price
for key in grocery_prices:
if key[0] in 'aeiouAEIOU':
article = 'an'
else:
article = 'a'
print(f"The price of {article} {key} is ${grocery_prices[key]}")
print('\n\n')
# print the dictionary with all price
for key, value in grocery_prices.items():
if key[0] in 'aeiouAEIOU':
article = 'an'
else:
article = 'a'
print(f"The price of {article} {key} is ${value}")
The price of an apple is $1.25 The price of a banana is $0.75 The price of an orange is $1.0 The price of a bread is $2.5 The price of a milk is $1.8 The price of an eggs is $2.2 The price of a chicken is $5.5 The price of a potatoes is $1.5 The price of a tomatoes is $2.0 The price of an onions is $0.8 The price of an apple is $1.25 The price of a banana is $0.75 The price of an orange is $1.0 The price of a bread is $2.5 The price of a milk is $1.8 The price of an eggs is $2.2 The price of a chicken is $5.5 The price of a potatoes is $1.5 The price of a tomatoes is $2.0 The price of an onions is $0.8
1) Fortran style loop: using range()###¶
In Fortran, a typical loop structure is known as a DO loop. In Python, you can achieve a similar loop structure using the range function. Here's an example of a simple Fortran-style DO loop in Python:
# Fortran-style loop
start = 1
end = 5
step = 1
for i in range(start, end + 1, step):
# Loop body
print(f"Current value: {i}")
In this example:
- start is the starting value of the loop.
- end is the ending value (exclusive) of the loop.
- step is the increment between values.
The range function generates a sequence of numbers from start to end - 1 with the specified step. The loop iterates over these values, and the loop body is executed for each iteration. If you want to achieve a Fortran-style loop where the loop index starts at 1 and ends at end, you can adjust the range parameters accordingly (default value for start and step are 0 and 1 respectivelly)
a= (-22.0, 3.5, 8.1, -10, 0.5)
# Fortran-style loop starting from 1
end = 5
for i in range(1, end + 1):
# Loop body
print(f"Current value: {i}, a[{i-1}] is equal to {a[i-1]:f}")
Current value: 1, a[0] is equal to -22.000000 Current value: 2, a[1] is equal to 3.500000 Current value: 3, a[2] is equal to 8.100000 Current value: 4, a[3] is equal to -10.000000 Current value: 5, a[4] is equal to 0.500000
2) Fortran style loop: using enumerate()¶
The enumerate function in Python is a useful utility for iterating over elements in an iterable (e.g., a list, tuple, or string) while also keeping track of the index or position of each element. It returns pairs of index and element during each iteration, making it convenient for scenarios where you need both the item and its index. Here's a brief explanation and example: Syntax:
enumerate(iterable, start=0)
iterable: The iterable to be enumerated.
start: (Optional) The starting value of the index. Default is 0.
Example:
fruits = ['apple', 'banana', 'orange', 'grape']
# Without enumerate
for i in range(len(fruits)):
print(i, fruits[i])
print('\n')
# Using enumerate
for index, fruit in enumerate(fruits):
print(index, fruit)
0 apple 1 banana 2 orange 3 grape 0 apple 1 banana 2 orange 3 grape
WHILE-Loop¶
A while loop or indefinite loop is a set of instructions that is repeated as long as the associated logical expression is True. The following is the syntax of a while loop block.
while <logical expression>:
# Code block to be repeated until logical statement is false
code block
# demonstrating a basic while-loop
total = 0
while total < 5:
total += 1 # equivalent to: `total = total + 1`
print(total) # `total` has the value 2
5
Further clauses in loop¶
In Python, loops (such as for and while loops) can be augmented with break, continue, and else clauses to control their behavior. Here's an explanation of each:
break Statement:¶
The break statement is used to exit a loop prematurely. When encountered, it terminates the loop immediately, and the control is transferred to the next statement following the loop.for i in range(5):
if i == 3:
break
print(i)
# Output: 0 1 2
continue Statement:¶
The continue statement is used to skip the rest of the code inside a loop for the current iteration and move to the next iteration.for i in range(5):
if i == 2:
continue
print(i)
# Output: 0 1 3 4
else Clause:¶
The else clause in a loop is executed when the loop condition becomes False. However, if the loop was terminated by a break statement, the else clause is skipped.for i in range(5):
print(i)
else:
print("Loop completed without a break")
# Output: 0 1 2 3 4 Loop completed without a break
for i in range(5):
if i == 2:
break
print(i)
else:
print("Loop completed without a break")
# Output: 0 1
These constructs provide control flow mechanisms within loops. break and continue allow you to alter the normal flow of the loop based on certain conditions, and the else clause in a loop can be used for code that should be executed after the loop has completed successfully (without encountering a break statement).
SOME PROGRAMMING EXAMPLE¶
Recursion¶
Very complex problem could be recurivelly break up on smaller handable problem. That is the base of functional program paradigm.
for instance a function calculatin factorial could be reduced to one line
factorial = lambda x: x1 if x==0 else x*factorial(x-1)
A more complex problem: The Tower of Hanoi¶
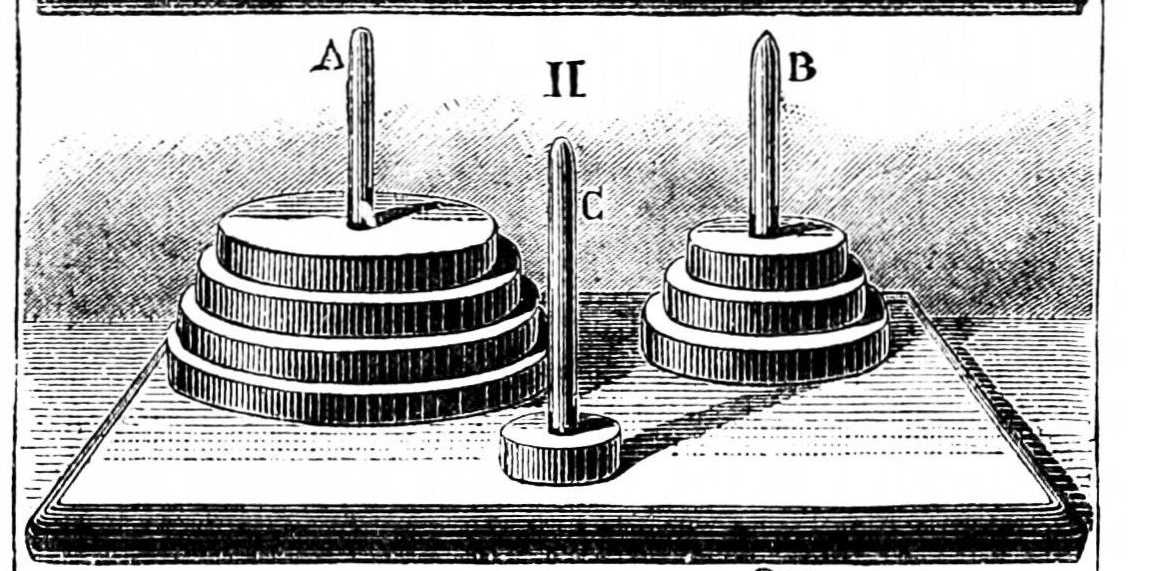
The Tower of Hanoi is a classic problem in computer science and recursion. It involves moving a tower of disks from one peg to another, subject to the following constraints:
*Only one disk can be moved at a time. *Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack or on an empty rod. *No disk may be placed on top of a smaller disk.
Explanation:
The hanoi function is a recursive function that takes the number of disks (n) and three pegs (source, target, and auxiliary) as parameters.
The base case (if n > 0) ensures that the recursion stops when there are no disks left to move.
The recursive calls move n-1 disks from the source peg to the auxiliary peg and then move the nth disk from the source peg to the target peg.
The function is called with the initial configuration of the Tower of Hanoi: hanoi(3, 'A', 'C', 'B'). This means there are 3 disks on peg 'A', and we want to move them to peg 'C' using peg 'B' as an auxiliary peg.
The output of the program shows the sequence of moves required to solve the Tower of Hanoi problem for 3 disks.
This implementation follows the recursive nature of the Tower of Hanoi problem, where the movement of a tower of disks is broken down into smaller sub-problems.
Here's a Python implementation of the Tower of Hanoi problem along with an explanation:
def hanoi(n, source, target, auxiliary):
"""
Solves the Tower of Hanoi problem using recursion.
Parameters:
- n: Number of disks.
- source: Source peg.
- target: Target peg.
- auxiliary: Auxiliary peg.
"""
###
###
###
###
# Example: Solve Tower of Hanoi for 3 disks
hanoi(3, 'A', 'C', 'B')
Move disk 1 from A to C Move disk 2 from A to B Move disk 1 from C to B Move disk 3 from A to C Move disk 1 from B to A Move disk 2 from B to C Move disk 1 from A to C
Iteration¶
The Fibonacci sequence is a series of numbers in which each number is the sum of the two preceding ones, usually starting with 0 and 1.iT is named after Leonardo of Pisa, an Italian mathematician also known as Fibonacci. He introduced the sequence to the Western world in his 1202 book "Liber Abaci."
The Fibonacci sequence is defined by the recurrence relation:
$[ F(n) = F(n-1) + F(n-2) $
with initial conditions ( F(0) = 0 ) and ( F(1) = 1 ). The sequence begins: ( 0, 1, 1, 2, 3, 5, 8, 13, 21, \ldots ).
Here's an example of the Fibonacci sequence using LaTeX in a mathematical context:
$ F(0) = 0, $
$ F(1) = 1, $
$ F(2) = F(1) + F(0) = 1 + 0 = 1, ] $
$ F(3) = F(2) + F(1) = 1 + 1 = 2, ] $
$ F(4) = F(3) + F(2) = 2 + 1 = 3, ] $
$ F(5) = F(4) + F(3) = 3 + 2 = 5, ] $
$ F(6) = F(5) + F(4) = 5 + 3 = 8, ] $
$ F(7) = F(6) + F(5) = 8 + 5 = 13, ] $
$ F(8) = F(7) + F(6) = 13 + 8 = 21, ] $
$ \ldots $
The Fibonacci sequence is often encountered in various mathematical and natural contexts, showcasing its significance and interesting properties.
The nature of series suggest a recursive approach
%%time
def fibonacci_recursive(n):
if n <= 1:
return n
else:
return fibonacci_recursive(n-1) + fibonacci_recursive(n-2)
# Example: Fibonacci sequence for n = 35
result_recursive = fibonacci_recursive(35)
print("\nRecursive Fibonacci:", result_recursive)
Recursive Fibonacci: 9227465 CPU times: total: 1.78 s Wall time: 1.78 s
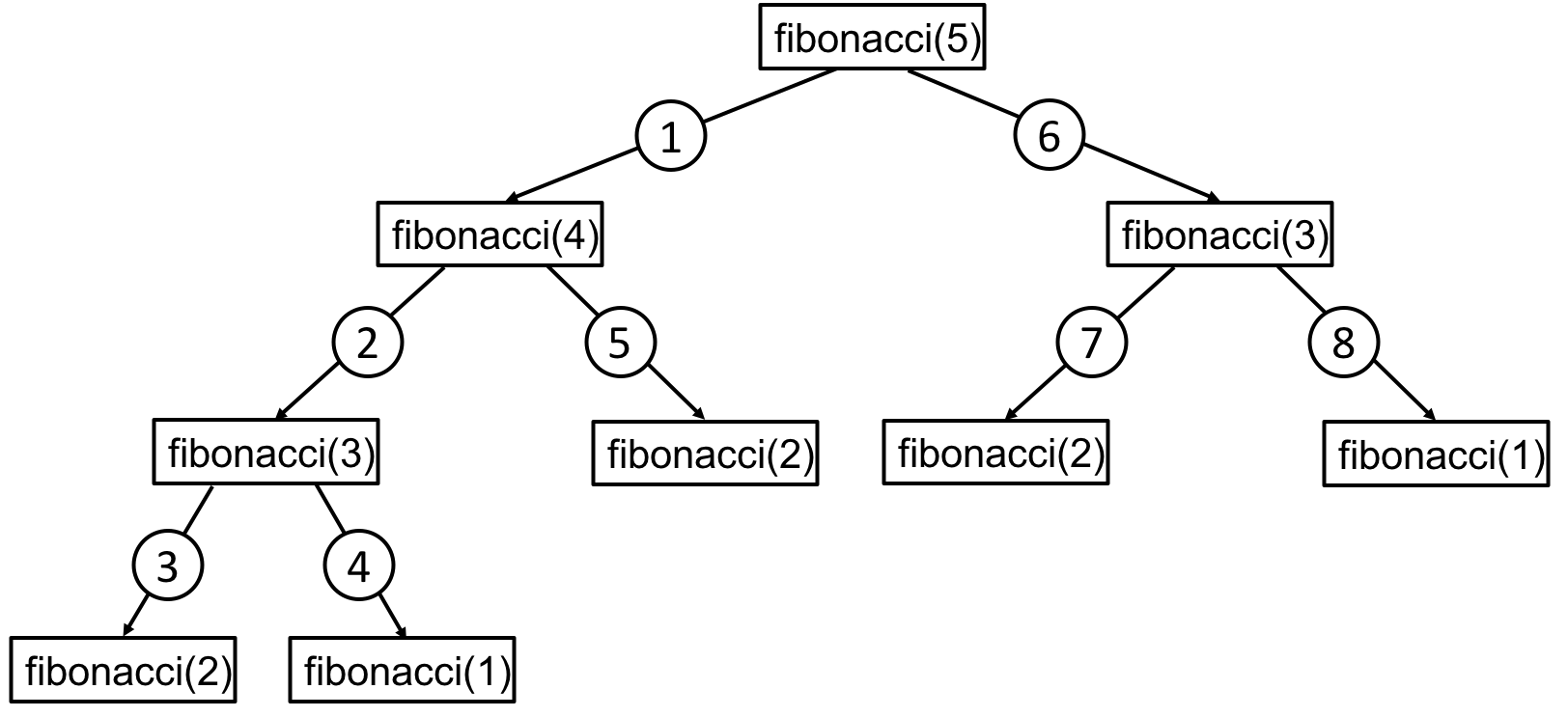
very slow for a small serie
indeed all call of the function launch two other evaluations
%%time
### Iterative Approach:
def fibonacci_iterative(n):
if n <= 1:
return n
a, b = 0, 1
for _ in range(n - 1):
a, b = b, a + b
return b
# Example: Fibonacci sequence for n = 35
result_iterative = fibonacci_iterative(35)
print("Iterative Fibonacci:", result_iterative)
Iterative Fibonacci: 9227465 CPU times: total: 0 ns Wall time: 0 ns
The recursive approach is concise and easy to understand, but it suffers from repeated calculations, leading to exponential time complexity. The iterative approach, using a loop, avoids redundancy and calculates each Fibonacci number once, resulting in linear time complexity. For small values of (n), both approaches may seem comparable. However, as (n) increases, the recursive approach becomes noticeably slower. Iteration is generally preferred for efficiency in such cases.
EXERCISE¶
the function pyXRD.pt_table.pt_p(Atom, 'At_w') return the atomic weight of an atom using such function create a function that return the molecular weight of a given formula